Selamat datang di blog jawabpedia.blogspot.com http://www.jawabpedia.blogspot.com/, Anda sedang membaca postingan yang berjudul "Belajar Mudah Persamaan Linier Dua Variabel ", dan jika anda beruntung, kemungkinan ada link download pada setiap postingan yang ada di blog ini, jika data yang anda cari tidak ada, silahkan cari di kotak pencarian di atas postingan, dan atau di bawah postingan (untuk view handphone dan atau smartphone). Nah untuk view destop atau PC atau laptop kotak pencarian ada di atas postingan dan samping kanan atas (sidebar) blog ini. oke deh.. selamat menikmati
Admin jawabpedia.blogspot.com
Admin jawabpedia.blogspot.com menyampaikan terimakasih atas kunjungan anda, jangan sungkan untuk berbagi, Anda masih membaca postingan yang berjudul "Belajar Mudah Persamaan Linier Dua Variabel " jika anda beruntung, akan anda link download ditiap-tiap postingan pada blog jawabpedia.blogspot.com. semoga bermanfaat...
Haloo, Teman-teman kali ini Agus Blog akan berbagi materi pelajaran matematika dengan judul "Belajar Mudah Persamaan Linier Dua Variabel" silahkan diikuti.........................
Berikut beberapa Contoh Soal nya :
Persamaan linear dua variabel adalah persamaan garis lurus yang mempunyai 2 variabel atau peubah.
Contoh:
Contoh:
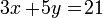→ persamaan dengan dua variabel x dan y.
→ persamaan dengan dua variabel α dan β.
Berikut beberapa Contoh Soal nya :
Soal 1
Diketahui sistem persamaan:
3x +2y=8 dan x – 5y = -37,
Nilai 6x + 4y adalah . . . .
a. -30
b. -16
c. 16
d. 30
Penyelesaian :
Gunakan metode subsitusi dan eliminasi.
3x + 2y = 8 x 1 à 3x + 2y = 8
x – 5y = -37 x 3 à 3x - 15y = -111
-------------------- -
17y = 119
y = 7
Subsitusikan nilai y = 7 ke persamaan (1)
3x + 2y = 8
3x + 2(7) = 8
3x + 14 = 8
3x = 8 – 14
3x = -6
x = -2
Nilai dari : 6x + 4y = 6(-2) + 4(7)
= -12 + 28
= 16.
Soal 2
Harga 8 buah buku tulis dan 6 buah pensil Rp 14.400,00. Harga 6 buah buku tulis dan 5 buah pensil Rp 11.200,00. Jumlah harga 5 buah buku tulis dan 8 buah pensil adalah . .
a. Rp 13.600,00
b. Rp 12.800,00
c. Rp 12.400,00
d. Rp 11.800,00
Penyelesaian :
Misal; buku tulis = x dan
pensil = y
8x + 6y = 14.400 x 3
6x + 5y = 11.200 x 4
24x + 18y = 43.200
24x + 20y = 44.800
_________________ -
-2y = - 1.600
y = 800
Subsitusikan nilai y = 800
6x + 5y = 11.200
6x + 5(800) = 11.200
6x + 4000 = 11.200
6x = 11.200 – 4000
6x = 7.200
x = 1.200
Nilai : 5x + 8y = 5(1.200) + 8(800)
= 6.000 + 6.400
= 12.400
Soal 3
Harga 4 ekor ayam dan 3 ekor itik
Rp 55.000,00 sedangkan harga 3 ekor ayam dan 5 ekor itik Rp 47.500,00.
Harga 1 ekor ayam dan 1 ekor itik berturut-turut adalah . . .
a. Rp 15.833,33 dan Rp 9.500,00
b. Rp 13.750,00 dan Rp 11.000,00
c. Rp 7.500,00 dan Rp 5.000,00
d. Rp 7.875, 14 dan Rp 4.750,00
Penyelesaian :
Misal : ayam = x dan itik = y
4x + 5y = 55.000
3x + 5y = 47.500
--------------------- ( - )
x = 7.500
Harga 1 ekor ayam = Rp 7.500,00
Subsitusikan nilai x = 7.500
4x + 5y = 55.000
5y = 55.000 – 4(7.500)
5y = 55.000 – 30.000
5y = 25.000
y = 5.000
Harga 1 ekor itik = Rp 5.000,00
Jadi :
Harga 1 ekor ayam = Rp 7.500,00
Harga 1 ekor itik = Rp 5.000,00
Soal 4
Pada sebuah tempat parkir terdapat 84 kendaraan yang terdiri dari sepeda motor dan mobil ( roda empat ). Setelah dihitung jumlah roda seluruhnya ada 220. Jika tarif parkir untuk sepeda motor Rp 300,00 dan untuk mobil Rp 500.00, maka besar uang parkir yang diterima tukang parkir tersebut adalah . . .
a. Rp 30.400,00
b. Rp 30.800,00
c. Rp 36.400,00
d. Rp 36.800,00
Penyelesaian :
Misal: motor = x dan mobil = y
x + y = 84 x 2 à 2x + 2y = 164
2x + 4y = 220 x 1 à 2x + 4y = 220
_____________ -
-2y = -56
y = 28
Banyak motor ( roda 2 ) = 28
Subsitusikan x = 28 pada persamaan (1)
x + y = 84
y = 84 – 28
y = 56
Banyak mobil = 56
Banyak uang parkir :
28x + 56y = 28(300) + 56(500)
= 8400 + 28000
= 36.400
Total uang parkir = Rp 36.400,00
Soal 5
Harga 3 pasang sepatu dan 5 buah tas adalah Rp 290.000,00. Sedangkan harga 4 pasang sepatu dan 2 buah tas Rp 200.000,00. Harga 3 pasang sepatu dan 2 buah tas adalah . . a.Rp 190.000,00
b.Rp 180.000,00
c.Rp 170.000,00
d.Rp 150.000,00
Penyelesaian :
Misal: sepatu = x dan tas = y
3x + 5y = 290.000 x 4
4x + 2y = 200.000 x 3
12x + 20y = 1.160.000
12x + 6y = 600.000
___________________ -
14 y = 560.000
y = 40.000
Subsitusikan nilai y = 40.000
4x + 2y = 200.000
4x = 200.000 - 2( 40.000)
4x = 120.000
x = 30.000
harga 3 ps sepatu dan 2 buah tas =
3x + 2y = 3(30.000) + 2( 40.000)
= 90.000 + 80.000
= 170.000
Jadi harganya = Rp 170.000,00
Soal 6
Harga 12 pensil dan 8 buku Rp 44.000,00 sedangkan harga 9 pensil dan 4 buku
Rp 31.000,00. Jumlah uang yang harus dibayarkan untuk 2 pensil dan 5 buku adalah . . .
a. Rp 11.000,00
b. Rp 15.000,00
c. Rp 17.000,00
d. Rp 21.000,00
Penyelesaian :
Misal: pensil = a dan buku = b
12 a + 8 b = 44.000 x 1
9 a + 4 b = 31.000 x 2
12 a + 8 b = 44.000
18 a + 8 b = 62.000
-------------------------- -
-6a = -18.000
a = 3.000
Subsitusikan nilai a = 3.000
12 a + 8 b = 44.000
8 b = 44.000 – 12( 3000 )
8 b = 8.000
b = 1.000
Harga 2 pensil dan 5 buku adalah :
2 ( 3.000 ) + 5 ( 1.000 )
6.000 + 5.000 = 11.000
Jadi yang harus dibayar =Rp 11.000,00
Soal 7
Harga 3 potong baju dan 4 potong celana Rp 450.000,00 sedangkan harga 5 potong baju dan 2 potong celana Rp 400.000,00. Harga 4 potong baju dan 5 potong celana adalah . . .
a. Rp 150.000,00
b. Rp 170.000,00
c. Rp 575.000,00
d. Rp 790.000,00
Penyelesaian :
Misal: baju = p dan celana = q
3 p + 4 q = 450.000 x 1
5 p + 2 q = 400.000 x 2
3 p + 4 q = 450.000
10 p + 4 q = 800.000
___________________ -
-7p = -350.000
p = 50.000
Subsitusikan nilai p = 50.000
3 p + 4 q = 450.000
4 q = 450.000 – 3( 50.000)
4 q = 450.000 - 150.000
q = 75.000
Harga 4 potong baju dan 5 potong celana:
= 4 ( 50.000 ) + 5 ( 75.000 )
= 200.000 + 375.000
= 575.000
Jadi Harganya =Rp 575.000,00
Soal 8
Pada suatu ladang terdapat 12 ekor hewan terdiri dari ayam dan kambing, sedangkan jumlah kaki hewan itu ada 40 buah. Banyak kambing di ladang tersebut adalah ...
a. 5 ekor
b. 6 ekor
c. 7 ekor
d. 8 ekor
Penyelesaian :
Misal : banyak ayam = x ekor
banyak kambing = y ekor
x + y = 12 x 2 à 2x + 2y = 24
2x + 4y = 40 x 1 à 2x + 4y = 40
-2y = -16
y = 8
Subsitusikan nilai y = 8 ke dalam persamaan :
x + y = 12
x = 12 - 8
x = 4
Jadi, banyak ayam = 4 ekor dan
kambing = 8 ekor.
Soal 9
Diketahui keliling sebuah persegi panjang adalah 70cm dan panjangnya 5 cm lebih dari lebarnya. Maka luas persegi panjang itu adalah ...
a. 300 cm2
b. 400 cm2
c. 500 cm2
d. 600 cm2
Penyelesaian :
Model matematikanya sbb :
P – l = 5 …………………………………. (1)
K = 2 ( p + l )
70 = 2 ( p + l ) à p + l = 35 …………(2)
Eliminasipersamaan(1) dan(2).
P – l = 5
P + l = 35
________ +
2p = 40 à p = 20
Subsitusikan nilai p = 20
P + l = 35
20 + l = 35
l = 35 – 20
l = 15
JadiLuaspersegipanjangadalah:
L = p x l = 20 x 15 = 300
0 komentar:
Posting Komentar